Chapitre 3 – Equations linéaires et quadratiques
Equations du premier degré à une inconnue avec des fractions
Lorsque l’on parle d’équation du premier degré, devant quelles sortes d’équations peux-tu te retrouver ?
- une équation simple du type ax + b = 0 : \[2x+3=0\]
- une équation un peu moins simple du type ax + b = cx + d : \[2x + 4 = -4x + 28\]
- une équation sous forme fractionnaire : \[\frac{x}{3}=\frac{4-x}{2}\]
- une équation rationnelle (avec l’inconnue au dénominateur) : \[\frac{x-2}{x-1}+\frac{1}{3}=1\]
→ attention dans ce cas à l’ensemble de définition
Ce cours traitera des équations sous forme fractionnaire, mais SANS inconnue au dénominateur.
Nous allons établir ensemble un guide pas à pas lorsque tu te trouves face à ce genre d’équations.
Prenons un exemple : \[\frac{x}{3}=\frac{4-x}{2}\]
Ici nous pouvons remarquer que nous avons des inconnues au numérateur de chaque fraction, ce qui nous dérange, donc on va d’abord se débarrasser de ces fractions.
Comment ?
En mettant tout au même dénominateur, le plus petit possible.
Dans ce cas, le plus petit dénominateur commun est : 3 • 2 = 6
\[\frac{2x}{6}=\frac{3(4-x)}{6}\]
Une fois que TOUT est au même dénominateur, on peut l’enlever.
\[2x = 3(4-x)\]
Puis on reprend le guide des équations de type ax + b = cx + d.
On développe d’abord.
\[2x = 12-3x\]
Puis si pas de simplification à faire de chaque côté du signe « = » alors on isole l’inconnue du côté gauche et le reste du côté droit.
\[2x +3x=12\]
\[5x=12\]
Finalement, on divise par le coefficient qui multiplie l’inconnue, si différent de 1.
On divise donc par 5, SANS changer le signe, car il s’agit d’une DIVISION.
\[x=\frac{12}{5}\]
La fraction est déjà irréductible, on la laisse comme cela.
\[S=\left \{ \frac{12}{5} \right \}\]
Le guide pas à pas aura donc deux étapes en plus.
Guide pas à pas
- TOUT mettre au même dénominateur de chaque côté du « = »
- Se débarrasser du dénominateur
- Effectuer tous les calculs de chaque côté du signe = → attention aux signes et aux priorités des opérations
- Réduire au maximum afin d’obtenir l’équation la plus simple possible.
- Isoler l’inconnue du côté gauche de préférence (avec le coefficient qui la multiplie, si différent de 1), ceci implique que les nombres « seuls » qui passent de l’autre côté doivent changer de signe, sauf s’il s’agit d’une division.
- Diviser par le coefficient qui la multiplie, si différent de 1.
- Noter la valeur de l’inconnue.
- Vérifier si on a trouvé la bonne valeur dans l’équation de départ.
Prenons encore un dernier exemple : \[x-1-\frac{2-x}{3}=\frac{3x}{4}\]
Pour se débarrasser des dénominateurs, on doit d’abord chercher le dénominateur commun le plus petit possible, ici ce sera 3 • 4 = 12
On met donc TOUT sur 12. Si vous n’êtes pas à l’aise avec cela, regardez le cours sur les fractions.
\[\frac{12x-12{\color{Red} -}4(2-x)}{12}=\frac{3(3x)}{12}\]
Puis on enlève les dénominateurs.
\[12x-12{\color{Red} -}4(2-x)=3(3x)\]
On simplifie.
\[12x-12-8+4x=9x\]
\[16x-20=9x\]
On regroupe les inconnues du côté gauche et le reste du côté droit, en faisant bien ATTENTION aux changements de signe.
\[16x-9x=20\]
\[7x=20\]
Puis on divise par le coefficient de l’inconnue, ici 7, SANS changer le signe car il s’agit d’une division.
\[x=\frac{20}{7}\]
La fraction est déjà irréductible, donc on la laisse comme cela.
\[S=\left \{\frac{20}{7} \right \}\]
Exercice corrigé n° 1
💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».
🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :
- On met les inconnues (ici x) à gauche et les chiffres à droite ;
- On isole x.
On passe 3 du côté droit (🧠 lorsqu’on passe un chiffre de l’autre côté du signe = et que l’on fait une addition/soustraction, le signe change) :
\[\frac{\color{red}6}{\color{red}5}x=\color{purple}-\color{green}3\]
Pour isoler l’inconnue on divise par le coefficient de l’inconnue du côté droit sans changer son signe :
\[x=\frac{\color{purple}-3}{\frac{\color{red}6}{\color{red}5}}\]
On multiplie ensuite par l’inverse (car diviser par une fraction c’est multiplier par l’inverse) :
\[x=\color{purple}-\frac{3}{1}\color{orange}\cdot \frac{\color{orange}5}{\color{orange}6}=\color{purple}-\frac{15}{6}\]
On rend la fraction irréductible en divisant le numérateur et le dénominateur par 3 :
\[x=\color{purple}-\frac{15}{6}=\color{purple}-\frac{5}{2}\]
On note la solution de cette équation :
\[S=\left \{ -\frac{5}{2} \right \}\]
Exercice corrigé n° 2
💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».
🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :
- On met les inconnues (ici x) à gauche et les chiffres à droite ;
- On isole x.
Tout d’abord, afin de faciliter la résolution on réécrit l’équation telle que :
\[\frac{\color{orange}1}{\color{orange}5}x-2=0\]
On passe 2 du côté droit (🧠 lorsqu’on passe un chiffre de l’autre côté du signe = et que l’on fait une addition/soustraction, le signe change) :
\[\frac{\color{red}1}{\color{red}5}x=\color{green}2\]
Pour isoler l’inconnue, on divise par le coefficient de l’inconnue du côté droit sans changer de signe :
\[x=\frac{2}{\frac{\color{red}1}{\color{red}5}}\]
On multiplie ensuite par l’inverse (car diviser par une fraction c’est multiplier par l’inverse) :
\[x=2\color{orange}\cdot \frac{\color{orange}5}{\color{orange}1}=10\]
On note la solution finale de cette équation :
\[S=\left \{ 10 \right \}\]
Exercice corrigé n° 3
💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».
🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :
- On met les inconnues (ici x) à gauche et les chiffres à droite ;
- On isole x.
Tout d’abord, afin de faciliter la résolution on réécrit l’équation telle que :
\[\frac{\color{orange}7}{\color{orange}4}x+2=0\]
On passe 2 du côté droit (🧠 lorsqu’on passe un chiffre de l’autre côté du signe = et que l’on fait une addition/soustraction, le signe change) :
\[\frac{\color{red}7}{\color{red}4}x=\color{purple}-\color{green}2\]
Pour isoler l’inconnue, on divise par le coefficient de l’inconnue du côté droit sans changer de signe :\[x=\frac{\color{purple}-2}{\frac{\color{red}7}{\color{red}4}}\]
On multiplie ensuite par l’inverse (car diviser par une fraction c’est multiplier par l’inverse) :
\[x=\color{purple}-2\color{orange}\cdot \frac{\color{orange}4}{\color{orange}7}=\frac{\color{purple}-8}{7}=-\frac{8}{7}\]
On note la solution finale de cette équation :
\[S=\left \{ -\frac{8}{7} \right \}\]
Exercice corrigé n° 4
💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».
🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :
- On met les inconnues (ici x) à gauche et les chiffres à droite ;
- On isole x.
Tout d’abord, afin de faciliter la résolution on réécrit l’équation telle que :
\[\color{orange}-\frac{\color{orange}1}{\color{orange}3}x-9=0\]
On passe 9 du côté droit (🧠 lorsqu’on passe un chiffre de l’autre côté du signe = et que l’on fait une addition/soustraction, le signe change) :
\[\color{red}-\frac{\color{red}1}{\color{red}3}x=\color{green}9\]
Pour isoler l’inconnue, on divise par le coefficient de l’inconnue du côté droit sans changer de signe :
\[x=\frac{9}{\color{red}-\frac{\color{red}1}{\color{red}3}}\]
On multiplie ensuite par l’inverse (car diviser par une fraction c’est multiplier par l’inverse) :
\[x=9\color{orange}\cdot (\color{orange}-\frac{\color{orange}3}{\color{orange}1})=\color{purple}-27\]
On note la solution finale de cette équation :
\[S=\left \{ -27 \right \}\]
Exercice corrigé n° 5
💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».
🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :
- On met les inconnues (ici x) à gauche et les chiffres à droite ;
- On isole x.
On passe les inconnues (ici x) à gauche et les chiffres à droite (⚠️ aux changements de signe) :
\[\frac{5}{3}x\color{teal}+\color{teal}9\color{teal}x=\frac{4}{3}\color{green}+\color{green}3\]
Ici comme on a des fractions « séparables » à gauche et à droite, mais qui ont toutes le même dénominateur, on met tout sur 3 qui est le plus petit dénominateur commun.
\[\frac{5}{3}x+\frac{9x\color{fuchsia}\cdot \color{fuchsia}3}{1\color{fuchsia}\cdot \color{fuchsia}3}=\frac{4}{3}+\frac{3 \color{fuchsia}\cdot \color{fuchsia}3}{1\color{fuchsia}\cdot \color{fuchsia}3}\]
Maintenant que tout est au même dénominateur à gauche et à droite, on s’en débarrasse :
\[\frac{5}{3}x+\frac{27}{3}x=\frac{4}{3}+\frac{9}{3}\leftrightarrow5x+27x=4+9\]
On simplifie en calculant à gauche et à droite :
\[\color{red}3\color{red}2x=13\]
Pour isoler l’inconnue, on divise par le coefficient de l’inconnue du côté droit sans changer de signe :
\[x=\frac{13}{\color{red}3\color{red}2}\]
On note la solution finale de cette équation :
\[S=\left \{ \frac{13}{32} \right \}\]
Exercice corrigé n° 6
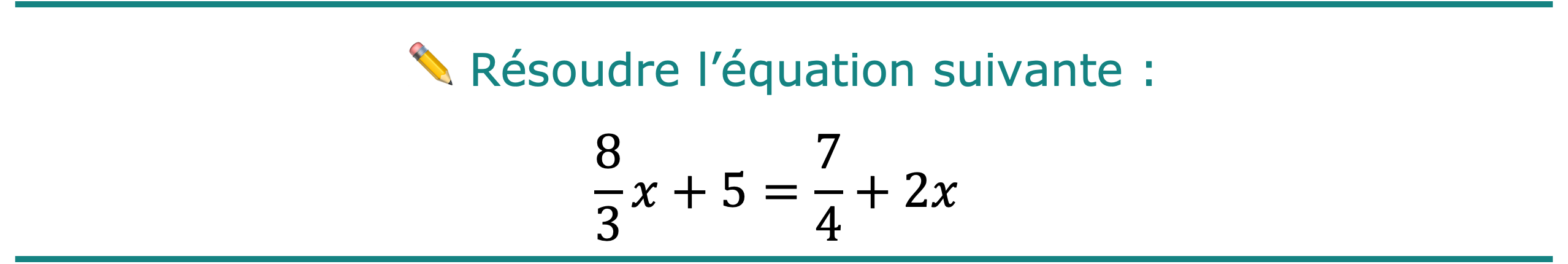
💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».
🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :
- On met les inconnues (ici x) à gauche et les chiffres à droite ;
- On isole x.
👀 Ici comme on a des fractions “séparables” à gauche et à droite qui n’ont pas le meme dénominateur, alors on a une option pour résoudre une telle équation :
- On met TOUT (à gauche et à droite) sur le même dénominateur et on s’en débarrasse.
On passe les inconnues (ici x) à gauche et les chiffres à droite (⚠️ aux changements de signe) :
\[\frac{8}{3}x\color{teal}-\color{teal}2\color{teal}x=\frac{7}{4}\color{green}-\color{green}5\]
On met TOUT (à gauche et à droite) sur le même dénominateur, le plus petit dénominateur commun (ici 3 ⋅ 4 = 12), afin de s’en débarrasser :
\[\frac{8 \color{fuchsia}\cdot \color{fuchsia} 4}{3 \color{fuchsia}\cdot \color{fuchsia} 4}x-\frac{2 \color{fuchsia}\cdot \color{fuchsia} 1\color{fuchsia}2}{1 \color{fuchsia}\cdot \color{fuchsia} 1\color{fuchsia}2}x=\frac{7 \color{fuchsia}\cdot \color{fuchsia} 3}{4 \color{fuchsia}\cdot \color{fuchsia} 3}-\frac{5 \color{fuchsia}\cdot \color{fuchsia} 1\color{fuchsia}2}{1 \color{fuchsia}\cdot \color{fuchsia} 1\color{fuchsia}2}\leftrightarrow\frac{32}{12}x-\frac{24}{12}x=\frac{21}{12}-\frac{60}{12}\]
Étant donné que l’ensemble des termes est maintenant au même dénominateur, alors on peut s’en débarrasser :
\[32x-24x=21-60\]
On simplifie en calculant à gauche et à droite :
\[\color{red}8x=-39\]
Pour isoler l’inconnue, on divise par le coefficient de l’inconnue du côté droit sans changer de signe :
\[x=\frac{-39}{\color{red}8}=-\frac{39}{8}\]
On note la solution finale de cette équation :
\[S=\left \{ -\frac{39}{8} \right \}\]
Exercice corrigé n° 7
💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».
🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :
- On met les inconnues (ici x) à gauche et les chiffres à droite ;
- On isole x.
Tout d’abord, afin de faciliter la résolution on réécrit l’équation telle que :
\[\color{orange}-\frac{\color{orange}7}{\color{orange}5}\color{orange}x-3=8+\frac{5}{10}x\]
👀 Ici comme on a des fractions “séparables” à gauche et à droite qui n’ont pas le meme dénominateur, alors on a une option pour résoudre une telle équation :
- On met TOUT (à gauche et à droite) sur le même dénominateur et on s’en débarrasse.
On passe les inconnues (ici x) à gauche et les chiffres à droite (⚠️ aux changements de signe) :
\[-\frac{7}{5}x\color{teal}-\frac{\color{teal}5}{\color{teal}1\color{teal}0}\color{teal}x=8\color{green} +\color{green}3\]
On met TOUT (à gauche et à droite) sur le même dénominateur, le plus petit dénominateur commun (ici 10), afin de s’en débarrasser :
\[-\frac{7\color{fuchsia} \cdot \color{fuchsia}2}{5 \color{fuchsia} \cdot \color{fuchsia}2}x-\frac{5}{10}x=\frac{8\color{fuchsia} \cdot \color{fuchsia}1\color{fuchsia}0}{1\color{fuchsia} \cdot \color{fuchsia}1\color{fuchsia}0}+\frac{3\color{fuchsia} \cdot \color{fuchsia}1\color{fuchsia}0}{1\color{fuchsia} \cdot \color{fuchsia}1\color{fuchsia}0}\leftrightarrow-\frac{14}{10}x-\frac{5}{10}x=\frac{80}{10}+\frac{30}{10}\]
Étant donné que l’ensemble des termes est maintenant au même dénominateur, alors on peut s’en débarrasser :
\[-14x-5x=80+30\]
On simplifie en calculant à gauche et à droite :
\[\color{red}-\color{red}1\color{red}9x=110\]
Pour isoler l’inconnue, on divise par le coefficient de l’inconnue du côté droit sans changer de signe :
\[x=\frac{110}{\color{red}-\color{red}1\color{red}9}=-\frac{110}{19}\]
On note la solution finale de cette équation :
\[S=\left \{ -\frac{110}{19} \right \}\]
Exercice corrigé n° 8
💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».
🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :
- On met les inconnues (ici x) à gauche et les chiffres à droite ;
- On isole x.
Tout d’abord, afin de faciliter la résolution on réécrit l’équation telle que :
\[\frac{\color{orange}9}{\color{orange}4}x-4=-\frac{7}{3}+9x\]
👀 Ici comme on a des fractions “séparables” à gauche et à droite qui n’ont pas le même dénominateur, alors on a une option pour résoudre une telle équation :
- On met TOUT (à gauche et à droite) sur le même dénominateur et on s’en débarrasse.
On passe les inconnues (ici x) à gauche et les chiffres à droite (⚠️ aux changements de signe) :
\[\frac{9}{4}x\color{teal}-\color{teal}9\color{teal}x=-\frac{7}{3}\color{green}+\color{green}4\]
On met TOUT (à gauche et à droite) sur le même dénominateur, le plus petit dénominateur commun (ici 10), afin de s’en débarrasser :
\[\frac{9 \color{fuchsia}\cdot \color{fuchsia}3}{4 \color{fuchsia} \cdot \color{fuchsia}3}x-\frac{9 \color{fuchsia}\cdot \color{fuchsia}1 \color{fuchsia}2}{1 \color{fuchsia} \cdot \color{fuchsia}1 \color{fuchsia}2}x=-\frac{7 \color{fuchsia} \cdot \color{fuchsia}4}{3 \color{fuchsia} \cdot \color{fuchsia}4}+\frac{4 \color{fuchsia} \cdot \color{fuchsia} 1 \color{fuchsia} \cdot \color{fuchsia}2}{1 \color{fuchsia} \cdot \color{fuchsia} 1 \color{fuchsia} \cdot \color{fuchsia}2}\leftrightarrow \frac{27}{12}x-\frac{108}{12}=-\frac{28}{12}+\frac{48}{12}\]
Étant donné que l’ensemble des termes est maintenant au même dénominateur, alors on peut s’en débarrasser :
\[27x-108x=-28+48\]
On simplifie en calculant à gauche et à droite :
\[\color{red}-\color{red}8\color{red}1x=20\]
Pour isoler l’inconnue, on divise par le coefficient de l’inconnue du côté droit sans changer de signe :
\[x=\frac{20}{\color{red}-\color{red}8\color{red}1 = -\frac{20}{81}}\]
On note la solution finale de cette équation :
\[S=\left \{ -\frac{20}{81} \right \}\]
Exercice corrigé n° 9
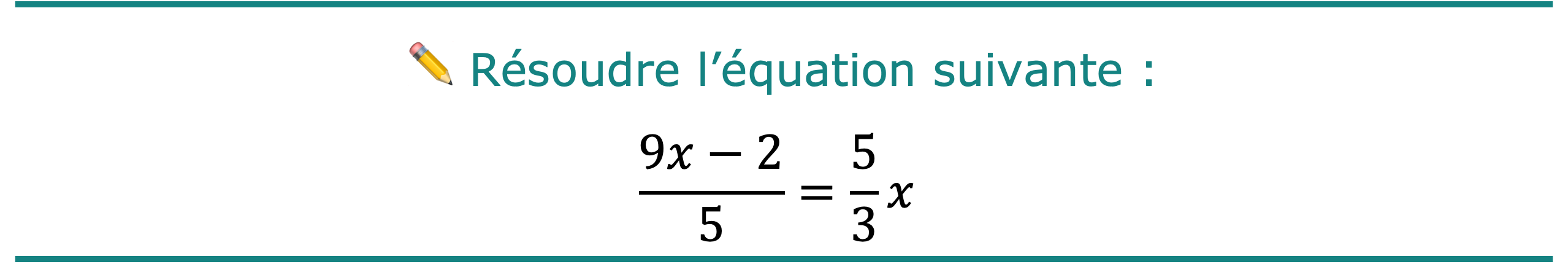
💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».
🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :
- On met les inconnues (ici x) à gauche et les chiffres à droite ;
- On isole x.
👀 Ici comme on a des fractions “non séparables”, alors on met TOUT sur le même dénominateur (le plus petit dénominateur commun) afin de s’en débarrasser et pouvoir isoler l’inconnue.
On met TOUT (à gauche et à droite) sur le même dénominateur, le plus petit dénominateur commun (ici 3 ⋅ 5 = 15), afin de s’en débarrasser :
\[\frac{\color{fuchsia}3\color{fuchsia}\cdot (9x-2)}{5 \color{fuchsia} \cdot \color{fuchsia} 3}=\frac{3 \color{fuchsia} \cdot \color{fuchsia} 5}{3 \color{fuchsia} \cdot \color{fuchsia} 5}x\]
Ensuite, on doit d’abord développer la parenthèse et effectuer les calculs :
\[\frac{27x-6}{\color{fuchsia}1\color{fuchsia}5}=\frac{25}{\color{fuchsia}1\color{fuchsia}5}x\]
Étant donné que l’ensemble des termes est maintenant au même dénominateur, alors on peut s’en débarrasser :
\[27x-6=25x\]
On passe les inconnues (ici x) à gauche et les chiffres à droite (⚠️ aux changements de signe) :
\[27x\color{teal}-\color{teal}2\color{teal}5\color{teal}x=\color{green}6\]
On simplifie en calculant à gauche et à droite :
\[\color{red}2x=6\]
Pour isoler l’inconnue, on divise par le coefficient de l’inconnue du côté droit sans changer de signe :
\[x=\frac{6}{\color{red}2}=3\]
On note la solution finale de cette équation :
\[S=\left \{ 3 \right \}\]
Exercice corrigé n° 10
💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».
🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :
- On met les inconnues (ici x) à gauche et les chiffres à droite ;
- On isole x.
👀 Ici comme on a des fractions “non séparables”, alors on met TOUT sur le même dénominateur (le plus petit dénominateur commun) afin de s’en débarrasser et pouvoir isoler l’inconnue.
On met TOUT (à gauche et à droite) sur le même dénominateur, le plus petit dénominateur commun (ici 4 ⋅ 3 = 12), afin de s’en débarrasser :
Ensuite, on doit d’abord développer la parenthèse et effectuer les calculs :
\[\frac{9x}{\color{fuchsia}1\color{fuchsia}2}=\frac{32-20x}{\color{fuchsia}1\color{fuchsia}2}\]
Étant donné que l’ensemble des termes est maintenant au même dénominateur, alors on peut s’en débarrasser :
\[9x=32-20x\]
On passe les inconnues (ici x) à gauche et les chiffres à droite (⚠️ aux changements de signe) :
\[9x\color{teal}+\color{teal}2\color{teal}0\color{teal}x=32\]
On simplifie en calculant à gauche et à droite :
\[\color{red}2\color{red}9x=32\]
Pour isoler l’inconnue, on divise par le coefficient de l’inconnue du côté droit sans changer de signe :
\[x=\frac{32}{\color{red}2\color{red}9}\]
On note la solution finale de cette équation :
\[S=\left \{ \frac{32}{29} \right \}\]
Exercice corrigé n° 11
💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».
🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :
- On met les inconnues (ici x) à gauche et les chiffres à droite ;
- On isole x.
👀 Ici comme on a des fractions “non séparables”, alors on met TOUT sur le même dénominateur (le plus petit dénominateur commun) afin de s’en débarrasser et pouvoir isoler l’inconnue.
On met TOUT (à gauche et à droite) sur le même dénominateur, le plus petit dénominateur commun (ici 5 ⋅ 2 = 10), afin de s’en débarrasser :
Ensuite, on doit d’abord développer la parenthèse et effectuer les calculs :
\[\frac{-14}{\color{fuchsia}1\color{fuchsia}0}x+\frac{20}{\color{fuchsia}1\color{fuchsia}0}=\frac{35-20x}{\color{fuchsia}1\color{fuchsia}0}\]
Étant donné que l’ensemble des termes est maintenant au même dénominateur, alors on peut s’en débarrasser :
\[-14x+20=35-20x\]
On passe les inconnues (ici x) à gauche et les chiffres à droite (⚠️ aux changements de signe) :
\[-14x\color{teal}+\color{teal}2\color{teal}0\color{teal}x=35\color{green}-\color{green}2\color{green}0\]
On simplifie en calculant à gauche et à droite :
\[\color{red}6x=15\]
Pour isoler l’inconnue, on divise par le coefficient de l’inconnue du côté droit sans changer de signe et on rend la fraction irréductible en divisant le numérateur et le dénominateur par 3 :
\[x=\frac{15}{\color{red}6}=\frac{5}{2}\]
On note la solution finale de cette équation :
\[S=\left \{ \frac{5}{2} \right \}\]
Exercice corrigé n° 12
💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».
🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :
- On met les inconnues (ici x) à gauche et les chiffres à droite ;
- On isole x.
⚡️ On a des parenthèses qui sont prioritaires sur les fractions.
👀 Ici comme on a des fractions “non séparables”, alors on met TOUT sur le même dénominateur (le plus petit dénominateur commun) afin de s’en débarrasser et pouvoir isoler l’inconnue.
La première étape est de développer la parenthèse du côté gauche :
\[\frac{8x+5}{2}+7=\frac{21x-6}{4}\]
Puis on met TOUT (à gauche et à droite) sur le même dénominateur, le plus petit dénominateur commun (ici 4), afin de s’en débarrasser :
Ensuite, on doit d’abord développer la parenthèse et effectuer les calculs :
\[\frac{16x+10}{\color{fuchsia}4}+\frac{28}{\color{fuchsia}4}=\frac{21x-6}{\color{fuchsia}4}\]
Étant donné que l’ensemble des termes est maintenant au même dénominateur, alors on peut s’en débarrasser :
\[16x+10+28=21x-6\]
On passe les inconnues (ici x) à gauche et les chiffres à droite (⚠️ aux changements de signe) :
\[16x\color{teal}-\color{teal}2\color{teal}1\color{teal}x=-6\color{green}-\color{green}1\color{green}0\color{green}-\color{green}2\color{green}8\]
On simplifie en calculant à gauche et à droite :
\[\color{red}-\color{red}5x=-44\]
Pour isoler l’inconnue, on divise par le coefficient de l’inconnue du côté droit sans changer de signe :
\[x=\frac{-44}{\color{red}-\color{red}5}=\frac{44}{5}\]
On note la solution finale de cette équation :
\[S=\left \{ \frac{44}{5} \right \}\]