Chapitre 3 – Equations linéaires et quadratiques

💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici x) à gauche et les chiffres à droite ;
• On isole x.

On passe les inconnues (ici x) à gauche et les chiffres du côté droit (⚠️ aux changements de signe) :

\[5x\color{teal}-\color{teal}2\color{teal}x=7\color{green}-\color{green}3\]

On simplifie en calculant à gauche et à droite :

\[\color{red}3x=4\]

Pour isoler l’inconnue, on divise par le coefficient de l’inconnue du côté droit sans changer de signe :

\[x=\frac{4}{\color{red}3}\]

On note la solution finale de cette équation :

\[S=\left \{ \frac{4}{3} \right \}\]

💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici x) à gauche et les chiffres à droite ;
• On isole x.

On passe les inconnues (ici x) à gauche et les chiffres du côté droit (⚠️ aux changements de signe) :

\[4x\color{purple}-\color{teal}2\color{teal}x=9\color{green}+\color{green}3\]

On simplifie en calculant à gauche et à droite :

\[\color{red}2x=12\]

Pour isoler l’inconnue, on divise par le coefficient de l’inconnue du côté droit sans changer de signe :

\[x=\frac{12}{\color{red}2}=6\]

On note la solution finale de cette équation :

\[S=\left \{ 6 \right \}\]

💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici x) à gauche et les chiffres à droite ;
• On isole x.

On passe les inconnues (ici x) à gauche et les chiffres du côté droit (⚠️ aux changements de signe) :

\[-7x\color{teal}+\color{teal}9\color{teal}x=3\color{green}+\color{green}4\]

On simplifie en calculant à gauche et à droite :

\[\color{red}2x=7\]

Pour isoler l’inconnue, on divise par le coefficient de l’inconnue du côté droit sans changer de signe :

\[x=\frac{7}{\color{red}2}\]

On note la solution finale de cette équation :

\[S=\left \{ \frac{7}{2} \right \}\]

💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici x) à gauche et les chiffres à droite ;
• On isole x.

On passe les inconnues (ici x) à gauche et les chiffres du côté droit (⚠️ aux changements de signe) :

\[5x\color{teal}-\color{teal}8\color{teal}x=-3\color{green}+\color{green}9\]

On simplifie en calculant à gauche et à droite :

\[\color{red}-\color{red}3x=6\]

Pour isoler l’inconnue, on divise par le coefficient de l’inconnue du côté droit sans changer de signe :

\[x=\frac{6}{\color{red}-\color{red}3}=-2\]

On note la solution finale de cette équation :

\[S=\left \{ -2 \right \}\]

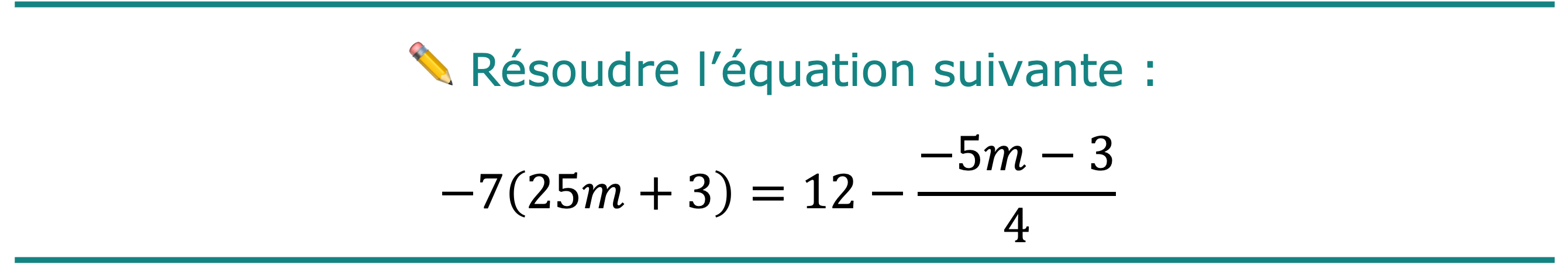
💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici m) à gauche et les chiffres à droite ;
• On isole m.

⚡️ Comme on a une parenthèse, alors on commence par la développer pour s’en débarrasser.

👀 Ici comme on a des fractions “non séparables”, alors on met TOUT sur le même dénominateur (le plus petit dénominateur commun) afin de s’en débarrasser et pouvoir isoler l’inconnue.

La première étape consiste à développer la parenthèse, en faisant très attention aux signes (⚠️ quand il y a un moins (-) devant une parenthèse, cela change les signes de la parenthèse) :

\[\color{purple}-175m\color{purple}-21=12-\frac{-5m-3}{4}\]

Puis on met TOUT (à gauche et à droite) sur le même dénominateur, le plus petit dénominateur commun (ici 4), afin de s’en débarrasser :

\[\frac{-175m\color{fuchsia}\cdot \color{fuchsia}4}{1 \color{fuchsia}\cdot \color{fuchsia}4}-\frac{21\color{fuchsia}\cdot \color{fuchsia}4}{1 \color{fuchsia}\cdot \color{fuchsia}4}=\frac{12\color{fuchsia}\cdot \color{fuchsia}4}{1 \color{fuchsia}\cdot \color{fuchsia}4}\color{purple}-\frac{-5m-3}{4}\leftrightarrow \frac{-700m}{4}-\frac{84}{4}=\frac{48}{4}-\frac{(-5m-3)}{4}\]

Étant donné que l’ensemble des termes est maintenant au même dénominateur, alors on peut s’en débarrasser (⚠️ quand il y a un moins (-) devant une fraction, cela change les signes du numérateur. 😁 Conseil pour ne pas l’oublier : mettre des parenthèses). On développe la parenthèse du côté droit :

\[-700m-84=48\color{purple}-(-5m-3)\leftrightarrow -700m-84=48\color{purple}+5m \color{purple}+3\]

On passe les inconnues (ici m) à gauche et les chiffres du côté droit (⚠️ aux changements de signe) :

\[-700m\color{teal}-\color{teal}5\color{teal}m=48+3\color{green}+\color{green}8\color{green}4\]

On simplifie en calculant à gauche et à droite :

\[\color{red}-\color{red}7\color{red}0\color{red}5m=135\]

Pour isoler l’inconnue on divise par le coefficient de l’inconnue du côté droit sans changer de signe et on rend la fraction irréductible en divisant le numérateur et le dénominateur par 15 :

\[x=\frac{135}{\color{red}-\color{red}7{\color{red}0}\color{red}5}=-\frac{9}{47}\]

On note la solution finale de l’équation :

\[S=\left \{ -\frac{9}{47} \right \}\]

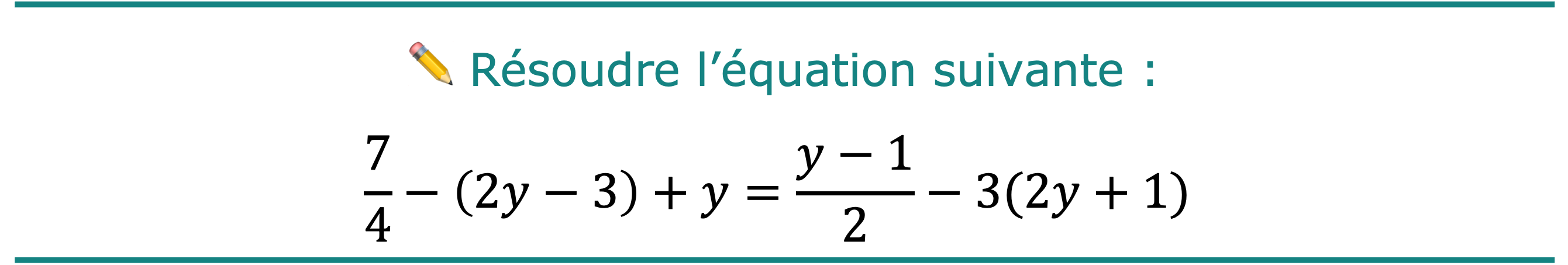
💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici y) à gauche et les chiffres à droite ;
• On isole y.

⚡️ Comme on a des parenthèses, alors on commence par les développer pour s’en débarrasser.

👀 Ici comme on a des fractions “non séparables”, alors on met TOUT sur le même dénominateur (le plus petit dénominateur commun) afin de s’en débarrasser et pouvoir isoler l’inconnue.

La première étape consiste à développer les parenthèses, en faisant très attention aux signes (⚠️ quand il y a un moins (-) devant une parenthèse, cela change les signes de la parenthèse) :

\[\frac{7}{4}\color{purple}-2y\color{purple}+3+y=\frac{y-1}{2}\color{purple}-6y\color{purple}-3\]

Puis on met TOUT (à gauche et à droite) sur le même dénominateur, le plus petit dénominateur commun (ici 4), afin de s’en débarrasser :

\[\frac{7}{4}-\frac{\color{fuchsia}4\color{fuchsia}\cdot(2y)}{1\color{fuchsia}\cdot \color{fuchsia}4}+\frac{3\color{fuchsia}\cdot\color{fuchsia}4}{1\color{fuchsia}\cdot \color{fuchsia}4}+\frac{y\color{fuchsia}\cdot\color{fuchsia}4}{1\color{fuchsia}\cdot \color{fuchsia}4}=\frac{\color{fuchsia}2\color{fuchsia}\cdot(y-1)}{2\color{fuchsia}\cdot\color{fuchsia}2}-\frac{\color{fuchsia}4\color{fuchsia}\cdot(6y)}{1\color{fuchsia}\cdot\color{fuchsia}4}-\frac{3\color{fuchsia}\cdot\color{fuchsia}4}{1\color{fuchsia}\cdot\color{fuchsia}4}\leftrightarrow \frac{7}{4}-\frac{8y}{4}+\frac{12}{4}+\frac{4y}{4}=\frac{2y-2}{4}-\frac{24y}{4}-\frac{12}{4}\]

Étant donné que l’ensemble des termes est maintenant au même dénominateur, alors on peut s’en débarrasser (⚠️ quand il y a un moins (-) devant une fraction, cela change les signes du numérateur. 😁 Conseil pour ne pas l’oublier : mettre des parenthèses). On développe la parenthèse du côté droit :

\[7-8y+12+4y=2y-2-24y-12\]

On passe les inconnues (ici y) à gauche et les chiffres du côté droit (⚠️ aux changements de signe) :

\[-8y+4y\color{teal}-\color{teal}2\color{teal}y\color{teal}+\color{teal}2\color{teal}4\color{teal}y=-2-12\color{green}-\color{green}7\color{green}-\color{green}1\color{green}2\]

On simplifie en calculant à gauche et à droite :

\[\color{red}1\color{red}8y=-33\]

Pour isoler l’inconnue on divise par le coefficient de l’inconnue du côté droit sans changer de signe et on rend la fraction irréductible en divisant le numérateur et le dénominateur par 3 :

\[x=\frac{-33}{\color{red}1\color{red}8}=-\frac{11}{6}\]

On note la solution finale de l’équation :

\[S=\left \{ -\frac{11}{6} \right \}\]

💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici x) à gauche et les chiffres à droite ;
• On isole x.

⚡️ Comme on a une parenthèse, alors on commence par la développer pour s’en débarrasser.

👀 Ici comme on a des fractions “non séparables”, alors on met TOUT sur le même dénominateur (le plus petit dénominateur commun) afin de s’en débarrasser et pouvoir isoler l’inconnue.

La première étape consiste à développer la parenthèse, en faisant très attention aux signes (⚠️ quand il y a un moins (-) devant une parenthèse, cela change les signes de la parenthèse) :

\[\frac{x-2}{8}\color{purple}-\frac{-5x-1}{3}=\frac{-x-9}{4}\color{purple}+3\color{purple}+\frac{\color{green}6}{\color{green}2}-10x\leftrightarrow \frac{x-2}{8}\color{purple}-\frac{-5x-1}{3}=\frac{-x-9}{4}\color{purple}+3-10x\]

Puis on met TOUT (à gauche et à droite) sur le même dénominateur, le plus petit dénominateur commun (ici 3 ⋅ 8 = 24), afin de s’en débarrasser :

\[\frac{\color{fuchsia}3\color{fuchsia}\cdot(x-2)}{8 \color{fuchsia}\cdot \color{fuchsia}3}\color{purple}-\frac{\color{fuchsia}8\color{fuchsia}\cdot(-5x-1)}{3 \color{fuchsia}\cdot \color{fuchsia}8}=\frac{\color{fuchsia}6\color{fuchsia}\cdot(-x-9)}{4 \color{fuchsia}\cdot \color{fuchsia}6}+\frac{3 \color{fuchsia}\cdot \color{fuchsia}2\color{fuchsia}4}{1 \color{fuchsia}\cdot \color{fuchsia}2\color{fuchsia}4}-\frac{{\color{fuchsia}2}{\color{fuchsia}4}{\color{fuchsia}\cdot}(10x)}{1 \color{fuchsia}\cdot \color{fuchsia}2\color{fuchsia}4}\]

Ensuite, on doit effectuer les calculs (développer les parenthèses) de chaque côté de l’équation (⚠️ quand il y a un moins (-) devant une fraction, cela change les signes du numérateur. 😁 Conseil pour ne pas l’oublier : mettre des parenthèses) :

\[\frac{3x-6}{24}\color{purple}-\frac{(-40x-8)}{24}=\frac{-6x-54}{24}+\frac{72}{24}-\frac{240x}{24}\]

Étant donné que l’ensemble des termes est maintenant au même dénominateur, alors on peut s’en débarrasser :

\[3x-6\color{purple}+40x\color{purple}+8=-6x-54+72-240x\]

On passe les inconnues (ici x) à gauche et les chiffres du côté droit (⚠️ aux changements de signe) :

\[3x+40x\color{teal}+\color{teal}6\color{teal}x\color{teal}+\color{teal}2\color{teal}4\color{teal}0\color{teal}x=-54+72\color{green}+\color{green}6\color{green}-\color{green}8\]

On simplifie en calculant à gauche et à droite :

\[\color{red}2\color{red}8\color{red}9x=16\]

Pour isoler l’inconnue on divise par le coefficient de l’inconnue du côté droit sans changer de signe :

\[x=\frac{16}{\color{red}2\color{red}8\color{red}9}\]

On note la solution finale de l’équation :

\[S=\left \{ \frac{16}{289} \right \}\]

💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici x) à gauche et les chiffres à droite ;
• On isole x.

⚡️ Ici on a plusieurs inconnues : x, y, a. Il faut donc faire très attention à l’inconnue dont on nous demande de trouver la valeur, ici on cherche x, donc on traitera y et a comme des « chiffres ».

La première étape consiste à développer la parenthèse, en faisant très attention aux signes (⚠️ quand il y a un moins (-) devant une parenthèse, cela change les signes de la parenthèse) :

\[9x\color{purple}-3y\color{purple}+6a=y-a+5x\]

On passe les inconnues (ici x) à gauche et les chiffres du côté droit (on considère que y et a sont des chiffres car on ne doit pas trouver leur valeur) – ⚠️ aux changements de signe :

\[9x-5x=y-a+3y-6a\]

On simplifie en calculant à gauche et à droite ce qui va ensemble :

\[\color{red}9\color{red}x\color{red}-\color{red}5\color{red}x=\color{orange}y\color{green}-\color{green}a\color{orange}+\color{orange}3\color{orange}y\color{green}-\color{green}6\color{green}a\leftrightarrow \color{red}4x={\color{orange}4}{\color{orange}y}-{\color{green}7}{\color{green}a}\]

Pour isoler l’inconnue on divise par le coefficient de l’inconnue du côté droit sans changer de signe :

\[x=\frac{4y-7a}{\color{red}4}\]

On simplifie la fraction :

\[x=\frac{\color{red}4y}{\color{red}4}-\frac{7a}{4}=y-\frac{7a}{4}\]

On note la solution finale de l’équation :

\[S=\left \{ y-\frac{7a}{4} \right \} \texttt{ou } S=\left \{ -\frac{7a}{4}+y \right \}\]

💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici s) à gauche et les chiffres à droite ;
• On isole s.

⚡️ Ici on a plusieurs inconnues : p, s, t. Il faut donc faire très attention à l’inconnue dont on nous demande de trouver la valeur, ici on cherche s, donc on traitera p et t comme des « chiffres ».

La première étape consiste à développer la parenthèse, en faisant très attention aux signes (⚠️ quand il y a un moins (-) devant une parenthèse, cela change les signes de la parenthèse) :

\[\color{purple}-7p\color{purple}-35s=s+t-9s\]

On passe les inconnues (ici s) à gauche et les chiffres du côté droit (on considère que p et t sont des chiffres car on ne doit pas trouver leur valeur) – ⚠️ aux changements de signe :

\[-35s-s+9s=t+7p\]

On simplifie en calculant à gauche ce qui va ensemble :

\[\color{red}-\color{red}3\color{red}5\color{red}s\color{red}-\color{red}s\color{red}+\color{red}9\color{red}s=t+7p\leftrightarrow \color{red}-\color{red}2\color{red}7s=\color{orange}t+\color{green}7\color{green}p\]

Pour isoler l’inconnue on divise par le coefficient de l’inconnue du côté droit sans changer de signe :

\[s=\frac{t+7p}{\color{red}-\color{red}2\color{red}7}\]

On simplifie la fraction :

\[s=\color{purple}-\frac{t}{27}\color{purple}-\frac{7p}{27}\]

On note la solution finale de l’équation :

\[S=\left \{ -\frac{t}{27} -\frac{7p}{27} \right \} \texttt{ ou } S=\left \{ -\frac{7p}{27} -\frac{t}{27} \right \}\]

💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici x) à gauche et les chiffres à droite ;
• On isole x.

⚡️ Ici on a plusieurs inconnues : x, t, m. Il faut donc faire très attention à l’inconnue dont on nous demande de trouver la valeur, ici on cherche x, donc on traitera t et m comme des « chiffres ».

La première étape consiste à développer la parenthèse, en faisant très attention aux signes (⚠️ quand il y a un moins (-) devant une parenthèse, cela change les signes de la parenthèse) :

\[-7x\color{purple}-15t\color{purple}+35mt=-x-3t\]

On passe les inconnues (ici x) à gauche et les chiffres du côté droit (on considère que t et m sont des chiffres car on ne doit pas trouver leur valeur) – ⚠️ aux changements de signe :

\[-7x+x=-3t+15t-35mt\]

On simplifie en calculant à gauche et à droite ce qui va ensemble :

\[\color{red}-\color{red}7\color{red}x\color{red}+\color{red}x=\color{orange}-\color{orange}3\color{orange}t\color{orange}+\color{orange}1\color{orange}5\color{orange}t\color{green}-\color{green}3\color{green}5\color{green}m\color{green}t\leftrightarrow \color{red}-\color{red}6x=\color{orange}1\color{orange}2\color{orange}t\color{green}-\color{green}3\color{green}5\color{green}m\color{green}t\]

Pour isoler l’inconnue on divise par le coefficient de l’inconnue du côté droit sans changer de signe :

\[x=\frac{12t-35mt}{\color{red}-\color{red}6}\]

On simplifie la fraction :

\[x=-\frac{\color{red}1\color{red}2t}{\color{red}6}+\frac{35mt}{6}\leftrightarrow x=-2t+\frac{35mt}{6}\]

On pourrait encore factoriser l’expression ; c’est-à-dire mettre le facteur t en évidence :

\[x=-2\color{blue}t+\frac{35m\color{blue}t}{6}\leftrightarrow x=\color{blue}t(-2+\frac{35m}6)\]

On note la solution finale de l’équation :

\[S=\left \{ -2t+\frac{35mt}{6} \right \} \texttt{ ou } S=\left \{ t(-2+\frac{35m}6 \right \}\]

💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici x) à gauche et les chiffres à droite ;
• On isole x.

On passe les inconnues (ici x) à gauche et les chiffres du côté droit (⚠️ aux changements de signe) :

\[3x\color{teal}-\color{teal}2\color{teal}x\color{teal}-\color{teal}x=4\color{green}+\color{green}5\]

On simplifie en calculant à gauche et à droite et on voit que les x se suppriment :

\[0x=9\leftrightarrow 0=9\]

❌ Cette équation n’est donc jamais vraie, car l’équation est impossible.

On note donc :

\[S=\left\{\emptyset\right\}\]

💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici x) à gauche et les chiffres à droite ;
• On isole x.

La première étape consiste à développer la parenthèse, en faisant très attention aux signes (⚠️ quand il y a un moins (-) devant une parenthèse, cela change les signes de la parenthèse) :

\[-6x+4=\color{purple}-6x\color{purple}+2\]

On passe les inconnues (ici x) à gauche et les chiffres du côté droit (⚠️ aux changements de signe) :

\[-6x\color{teal}+\color{teal}6\color{teal}x=2\color{green}-\color{green}4\]

On simplifie en calculant à gauche et à droite et on voit que les x se suppriment :

\[0x=-2\leftrightarrow 0=-2\]

❌ Cette équation n’est donc jamais vraie, car l’équation est impossible.

On note donc :

\[S=\left\{\emptyset\right\}\]

💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici x) à gauche et les chiffres à droite ;
• On isole x.

La première étape consiste à développer la parenthèse, en faisant très attention aux signes (⚠️ quand il y a un moins (-) devant une parenthèse, cela change les signes de la parenthèse) :

\[6x-4=6x\color{purple}-4\]

On voit déjà qu’on a exactement la même chose à gauche et à droite mais on passe quand même les inconnues (ici x) à gauche et les chiffres du côté droit (⚠️ aux changements de signe) :

\[6x\color{teal}-\color{teal}6\color{teal}x=-4\color{green}+\color{green}4\]

On simplifie en calculant à gauche et à droite :

\[0x=0\leftrightarrow 0=0\]

🔥 Cette expression est donc toujours vraie, car il y a une infinité de solutions possibles. L’équation est indéterminée.

On note donc :

\[S=\left\{\mathbb{R}\right\}\]

💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici x) à gauche et les chiffres à droite ;
• On isole x.

👀 Ici comme on a des fractions “non séparables”, alors on met TOUT sur le même dénominateur (le plus petit dénominateur commun) afin de s’en débarrasser et pouvoir isoler l’inconnue.

On met TOUT (à gauche et à droite) sur le même dénominateur, le plus petit dénominateur commun (ici 3), afin de s’en débarrasser :

\[\frac{\color{fuchsia}3\color{fuchsia} \cdot(3x-2)}{1 \color{fuchsia} \cdot \color{fuchsia}3}=\frac{9x-6}{3}\leftrightarrow \frac{9x-6}{3}=\frac{9x-6}{3}\]

Étant donné que l’ensemble des termes est maintenant au même dénominateur, alors on peut s’en débarrasser :

\[9x-6=9x-6\]

On voit déjà qu’on a exactement la même chose à gauche et à droite mais on passe quand même les inconnues (ici x) à gauche et les chiffres du côté droit (⚠️ aux changements de signe) :

\[9x\color{teal}-\color{teal}9\color{teal}x=-6\color{green}+\color{green}6\]

On simplifie en calculant à gauche et à droite :

\[0x=0\leftrightarrow 0=0\]

🔥 Cette expression est donc toujours vraie, car il y a une infinité de solutions possibles. L’équation est indéterminée.

On note donc :

\[S=\left\{\mathbb{R}\right\}\]

💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici s) à gauche et les chiffres à droite ;
• On isole s.

Comme on a des parenthèses, la première étape consiste à développer ces parenthèses afin de s’en débarrasser. On commence par développer (s – 2)². Pour cela, on a 2 options :

Option a : utiliser les identités remarquables

soit (s – 2)² = (a – b)² avec (a – b)² = a² – 2ab + b²

\[(\color{lime}s-\color{blue}2)^2=\color{lime}s^2-(2 \cdot \color{lime}s \cdot \color{blue}2)+\color{blue}2^2=\color{lime}s^2-4s+\color{blue}4\]

Option b : faire sans les identités remarquables, c’est-à-dire simplement en développant les parenthèses

soit (s – 2)² = (s – 2)(s – 2) :

\[(\color{lime}s-\color{blue}2)(\color{lime}s-\color{blue}2)=\color{lime}s^2-2s-2s+\color{blue}4=\color{lime}s^2-4s+\color{blue}4\]

On remplace dans notre équation et on développe la parenthèse à droite (ici ce n’est pas une identité remarquable) :

\[s^2-4s+4-8+s=s^2-6s\]

Ensuite, on passe les inconnues (ici s) à gauche et les chiffres à droite (⚠️ aux changements de signe) :

\[\color{navy}s^\color{navy}2\color{navy}-\color{navy}s^\color{navy}2\color{lime}-\color{lime}4\color{lime}s\color{lime}+\color{lime}6\color{lime}s=\color{green}-\color{green}4\color{green}+\color{green}8\]

On simplifie en calculant à gauche et à droite et les s² se suppriment – sinon nous n’aurions pas eu une équation linéaire (du 1^er degré) :

\[\color{red}3s=4\]

Pour isoler l’inconnue, on divise par le coefficient de l’inconnue du côté droit sans changer de signe :

\[s=\frac{4}{\color{red}3}\]

On note la solution finale de l’équation :

\[S=\left \{ \frac{4}{3} \right \}\]

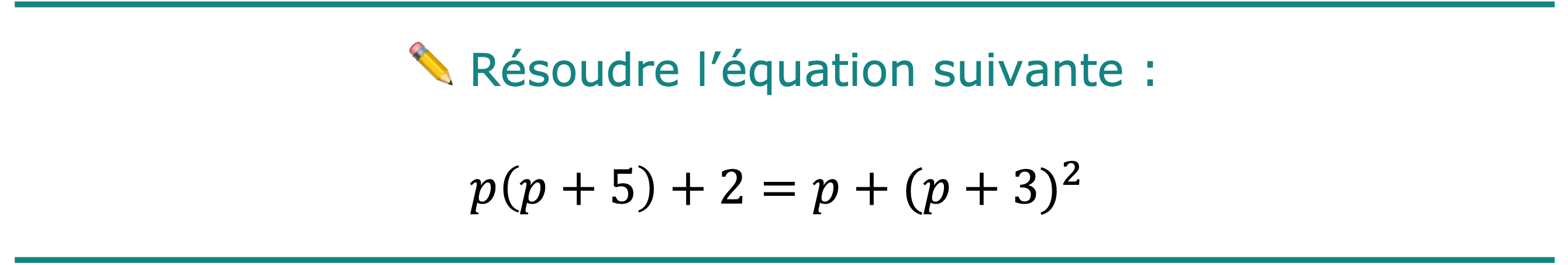
💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici p) à gauche et les chiffres à droite ;
• On isole p.

Comme on a des parenthèses, la première étape consiste à développer ces parenthèses afin de s’en débarrasser. On commence par développer (p + 3)². Pour cela, on a 2 options :

Option a : utiliser les identités remarquables

soit (p + 3)² = (a + b)² avec (a + b)² = a² + 2ab + b²

\[(\color{lime}p+\color{blue}3)^2=\color{lime}p^2+(2 \cdot \color{lime}p \cdot \color{blue}3)+\color{blue}3^2=\color{lime}p^2+6p+\color{blue}9\]

Option b : faire sans les identités remarquables, c’est-à-dire simplement en développant les parenthèses

soit (p + 3)² = (p + 3)(p + 3) :

\[(\color{lime}p+\color{blue}3)(\color{lime}p+\color{blue}3)=\color{lime}p^2+3p+3p+\color{blue}4=\color{lime}p^2+6p+\color{blue}9\]

On remplace dans notre équation et on développe la parenthèse à gauche (ici ce n’est pas une identité remarquable) :

\[p^2+p+2=p+p^2+6p+9\]

Ensuite, on passe les inconnues (ici p) à gauche et les chiffres à droite (⚠️ aux changements de signe) :

\[\color{navy}p^\color{navy}2\color{navy}-\color{navy}p^\color{navy}2\color{lime}+\color{lime}5\color{lime}p\color{lime}-\color{lime}p\color{lime}-\color{lime}6\color{lime}p=\color{green}9\color{green}-\color{green}2\]

On simplifie en calculant à gauche et à droite et les p² se suppriment – sinon nous n’aurions pas eu une équation linéaire (du 1^er degré) :

\[\color{red}-\color{red}2p=7\]

Pour isoler l’inconnue, on divise par le coefficient de l’inconnue du côté droit sans changer de signe :

\[p=\color{purple}-\frac{7}{\color{red}2}\]

On note la solution finale de l’équation :

\[S=\left \{ -\frac{7}{2} \right \}\]

💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici t) à gauche et les chiffres à droite ;
• On isole t.

Comme on a des parenthèses, la première étape consiste à développer ces parenthèses afin de s’en débarrasser. On commence par développer (2t – 4)². Pour cela, on a 2 options :

Option a : utiliser les identités remarquables

soit (2t – 4)² = (a – b)² avec (a – b)² = a² – 2ab + b²

\[(\color{lime}2\color{lime}t-\color{blue}4)^2=\color{lime}2^2\color{lime}t^2-(2 \cdot \color{lime}2\color{lime}t \cdot \color{blue}4)+\color{blue}4^2=\color{lime}4\color{lime}t^2-16t+\color{blue}1\color{blue}6\]

Option b : faire sans les identités remarquables, c’est-à-dire simplement en développant les parenthèses

soit (2t – 4)² = (2t – 4)(2t – 4) :

\[(\color{lime}2\color{lime}t-\color{blue}4)(\color{lime}2\color{lime}t-\color{blue}4)=\color{lime}4\color{lime}t^2-4t-4t+\color{blue}1\color{blue}6=\color{lime}4\color{lime}t^2-8t+\color{blue}16\]

On développe ensuite la parenthèse à droite. Pour cela on a l’option suivante :

Option a : utiliser les identités remarquables

soit (t – 6)(t + 6) = (a – b)(a + b) avec (a – b)(a + b) = a² – b²

\[(\color{lime}t-\color{blue}6)(\color{lime}t+\color{blue}6)=\color{lime}t^2-\color{blue}6^2=\color{lime}t^2-\color{blue}3\color{blue}6\]

On remplace dans notre équation et on développe la parenthèse à gauche (ici ce n’est pas une identité remarquable) :

\[4t^2-8t+16+6t=5t^2\color{purple}-(t^2-36)\leftrightarrow 4t^2-8t+16+6t=5t^2-t^2+36\]

Ensuite, on passe les inconnues (ici t) à gauche et les chiffres à droite (⚠️ aux changements de signe) :

\[\color{navy}4\color{navy}t^\color{navy}2-\color{navy}5\color{navy}t^\color{navy}2\color{navy}+\color{navy}t^\color{navy}2\color{lime}-\color{lime}1\color{lime}6\color{lime}t\color{lime}+\color{lime}6\color{lime}t=\color{green}3\color{green}6\color{green}-\color{green}1\color{green}6\]

On simplifie en calculant à gauche et à droite et les t² se suppriment – sinon nous n’aurions pas eu une équation linéaire (du 1^er degré) :

\[\color{red}-\color{red}1\color{red}0t=20\]

Pour isoler l’inconnue, on divise par le coefficient de l’inconnue du côté droit sans changer de signe :

\[t=\frac{20}{\color{red}-\color{red}1\color{red}0}\leftrightarrow t=-2\]

On note la solution finale de l’équation :

\[S=\left \{ -2 \right \}\]

💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici x) à gauche et les chiffres à droite ;
• On isole x.

⚡️ Avec un tel problème, il y a 2 étapes principales :

1️⃣ On isole x pour trouver sa valeur (qui dépendra de m)

2️⃣ On évalue la réponse obtenue pour x en fonction du paramètre m (on regarde ce que l’on obtient suivant la valeur attribuée à m)

Étape 1 : isoler x

La première étape consiste à développer la parenthèse, en faisant très attention aux signes (⚠️ quand il y a un moins (-) devant une parenthèse, cela change les signes de la parenthèse) :

\[3m\color{purple}+21mx-5mx+2=3m\]

On passe les inconnues (ici x) à gauche et les chiffres du côté droit (on considère que m est un chiffre car on ne doit pas trouver sa valeur) – ⚠️ aux changements de signe :

\[21mx-5mx=3m\color{green}-\color{green}2\color{orange}-\color{orange}3\color{orange}m\]

On simplifie en calculant à gauche et à droite ce qui va ensemble :

\[\color{red}1\color{red}6\color{red}mx=-2\]

Pour isoler l’inconnue on divise par le coefficient de l’inconnue du côté droit sans changer de signe :

\[x=\frac{-2}{\color{red}1\color{red}6\color{red}m}\leftrightarrow x=-\frac{2}{16m}\]

On note la solution finale de l’équation :

\[S=\left \{ -\frac{2}{16m} \right \}\]

Étape 2 : évaluer en fonction de m

Si m = 0 (on remplace donc m par 0) : 

\[x=-\frac{2}{16\color{red}\cdot \color{red}0}\leftrightarrow S=\emptyset\]

Si m ≠ 0 (on remplace m par n’importe quel chiffre entre ] – ∞ ; + ∞ [ sauf 0 ; par exemple -3) :

\[x=-\frac{2}{16\color{red}\cdot \color{red}(\color{red}-\color{red}3\color{red})}\leftrightarrow x=-\frac{2}{-48}\leftrightarrow x=\frac{1}{24}\]

👉 En résumé : lorsque m ≠ 0, peu importe sa valeur, l’équation aura une solution unique. Mais lorsque m = 0 alors on obtient 0 au dénominateur, ce qui est interdit, donc l’équation est impossible, elle n’a pas de solution.

⚡️ Réponse : Le paramètre m doit être égal à 0 pour que l’équation n’ait pas de solution.

💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici x) à gauche et les chiffres à droite ;
• On isole x.

⚡️ Avec un tel problème, il y a 2 étapes principales :

1️⃣ On isole x pour trouver sa valeur (qui dépendra de m)

2️⃣ On évalue la réponse obtenue pour x en fonction du paramètre m (on regarde ce que l’on obtient suivant la valeur attribuée à m)

Étape 1 : isoler x

La première étape consiste à développer la parenthèse, en faisant très attention aux signes (⚠️ quand il y a un moins (-) devant une parenthèse, cela change les signes de la parenthèse) :

\[-9mx-5\color{purple}+32mx\color{purple}-8m=2mx-8m\]

On passe les inconnues (ici x) à gauche et les chiffres du côté droit (on considère que m est un chiffre car on ne doit pas trouver sa valeur) – ⚠️ aux changements de signe :

\[-9mx+32mx\color{red}-\color{red}2\color{red}m\color{red}x=-8m\color{green}+\color{green}5\color{orange}+\color{orange}8\color{orange}m\]

On simplifie en calculant à gauche et à droite ce qui va ensemble :

\[\color{red}-\color{red}2\color{red}1\color{red}mx=5\]

Pour isoler l’inconnue on divise par le coefficient de l’inconnue du côté droit sans changer de signe :

\[x=\frac{5}{\color{red}-\color{red}2\color{red}1\color{red}m}\leftrightarrow x=-\frac{5}{21m}\]

On note la solution finale de l’équation :

\[S=\left \{ -\frac{5}{21m} \right \}\]

Étape 2 : évaluer en fonction de m

Si m = 0 (on remplace donc m par 0) :

\[x=-\frac{5}{21\color{red}\cdot \color{red}0}\leftrightarrow S=\emptyset\]

Si m ≠ 0 (on remplace m par n’importe quel chiffre entre ] – ∞ ; + ∞ [ sauf 0 ; par exemple 2) :

\[x=-\frac{5}{21\color{red}\cdot \color{red}2}\leftrightarrow x=-\frac{5}{42}\]

👉 En résumé : lorsque m ≠ 0, peu importe sa valeur, l’équation aura une solution unique. Mais lorsque m = 0 alors on obtient 0 au dénominateur, ce qui est interdit, donc l’équation est impossible, elle n’a pas de solution.

⚡️ Réponse : Le paramètre m n’a aucune valeur possible pour que l’équation admette tout réel pour solution.

💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici x) à gauche et les chiffres à droite ;
• On isole x.

⚡️ Avec un tel problème, il y a 2 étapes principales :

1️⃣ On isole x pour trouver sa valeur (qui dépendra de m)

2️⃣ On évalue et discute en fonction de m (on regarde ce que l’on obtient suivant la valeur attribuée à m)

Étape 1 : isoler x

On passe les inconnues (ici x) à gauche et les chiffres du côté droit (on considère que m est un chiffre car on ne doit pas trouver sa valeur) – ⚠️ aux changements de signe :

\[m^2x\color{red}-\color{red}2\color{red}5\color{red}x=3m+7\color{orange}+\color{orange}5\color{orange}m\color{green}+\color{green}4\]

On simplifie en calculant à gauche et à droite ce qui va ensemble :

\[m^2x-25x=8m+11\]

On factorise l’expression à gauche pour pouvoir isoler x plus facilement ; c’est-à-dire qu’on met le facteur x en évidence :

Pour isoler l’inconnue, on divise par le coefficient de l’inconnue du côté droit sans changer de signe :

\[x=\frac{8m+11}{\color{red}m^\color{red}2\color{red}-\color{red}2\color{red}5}\]

On remarque que l’on peut factoriser l’expression au dénominateur (💡 plus facile pour évaluer le paramètre m), avec une identité remarquable du type : a² – b² = (a + b)(a – b) :

Si m = 5 (on remplace donc m par 5) :

\[x=\frac{(8\color{red}\cdot \color{red}5)+11}{\color{red}5^\color{red}2-25}\leftrightarrow x=\frac{51}{0}\leftrightarrow S=\emptyset\]

Si m = -5 (on remplace donc m par -5) :

\[x=\frac{(8\color{red}\cdot \color{red}( \color{red}-\color{red}5\color{red}))+11}{\color{red}(\color{red}-\color{red}5\color{red})^\color{red}2\color{red}-25}\leftrightarrow x=-\frac{29}{0}\leftrightarrow S=\emptyset\]

Si m ≠ ±5 (on remplace par exemple m par 4) :

\[x=\frac{(8\color{red}\cdot \color{red}4)+11}{\color{red}(\color{red}4^\color{red}2\color{red})-25}\leftrightarrow x=-\frac{43}{9}\]

👉 En résumé : Lorsque m ≠ ±5, peu importe sa valeur, l’équation aura une solution unique. Mais lorsque m = 5 ou -5 alors on obtient 0 au dénominateur, ce qui est interdit, donc l’équation est impossible, elle n’a pas de solution.

⚡️ Réponse : L’équation aura toujours une solution si m ≠ ±5.

💡 On utilisera dorénavant toujours le « raccourci », que l’on a appelé la méthode « gauche/droite ».

🧠 La méthode « gauche/droite » est une automatisation pour aller plus vite. Elle se résume à 2 étapes :

• On met les inconnues (ici x) à gauche et les chiffres à droite ;
• On isole x.

⚡️ Avec un tel problème, il y a 2 étapes principales :

1️⃣ On isole x pour trouver sa valeur (qui dépendra de m)

2️⃣ On évalue et discute en fonction de m (on regarde ce que l’on obtient suivant la valeur attribuée à m)

Étape 1 : isoler x

On passe les inconnues (ici x) à gauche et les chiffres du côté droit (on considère que m est un chiffre car on ne doit pas trouver sa valeur) – ⚠️ aux changements de signe :

\[m^2x\color{red}-\color{red}1\color{red}6\color{red}x=8\color{orange}-\color{orange}3\color{orange}m\color{green}+\color{green}4\]

On simplifie en calculant à gauche et à droite ce qui va ensemble :

\[m^2x-16x=-3m+12\]

On factorise l’expression à gauche pour pouvoir isoler x plus facilement ; c’est-à-dire qu’on met le facteur x en évidence :

Pour isoler l’inconnue, on divise par le coefficient de l’inconnue du côté droit sans changer de signe :

\[x=\frac{-3m+12}{\color{red}m^\color{red}2\color{red}-\color{red}1\color{red}6}\]

On remarque que l’on peut factoriser l’expression au dénominateur (💡 plus facile pour évaluer le paramètre m), avec une identité remarquable du type : a² – b² = (a + b)(a – b) :

Si m = 4 (on remplace donc m par 4) :

\[x=\frac{(-3\color{red}\cdot \color{red}4)+12}{\color{red}4^\color{red}2-16}\leftrightarrow x=\frac{0}{0}\leftrightarrow S=\mathbb{R}\]

Si m = -4 (on remplace donc m par -4) :

\[x=\frac{(-3\color{red}\cdot \color{red}(\color{red}-\color{red}4\color{red}))+12}{\color{red}(\color{red}-\color{red}4\color{red})^\color{red}2-16}\leftrightarrow x=\frac{24}{0}\leftrightarrow S=\emptyset\]

Si m ≠ ±4 (on remplace par exemple m par 2) :

\[x=\frac{(-3\color{red}\cdot \color{red}2)+12}{\color{red}(\color{red}2\color{red})^\color{red}2-16}\leftrightarrow x=-\frac{1}{2}\]

👉 En résumé : Lorsque m ≠ ±4, peu importe sa valeur, l’équation aura une solution unique. Mais lorsque m = -4 alors on obtient 0 au dénominateur, ce qui est interdit, donc l’équation est impossible, elle n’a pas de solution. Et finalement, lorsque m = 4, alors tout nombre réel est solution de l’équation.

⚡️ Réponse : L’équation aura toujours une solution si m ≠ ±4 et si m = 4, alors tout nombre réel est solution de l’équation.